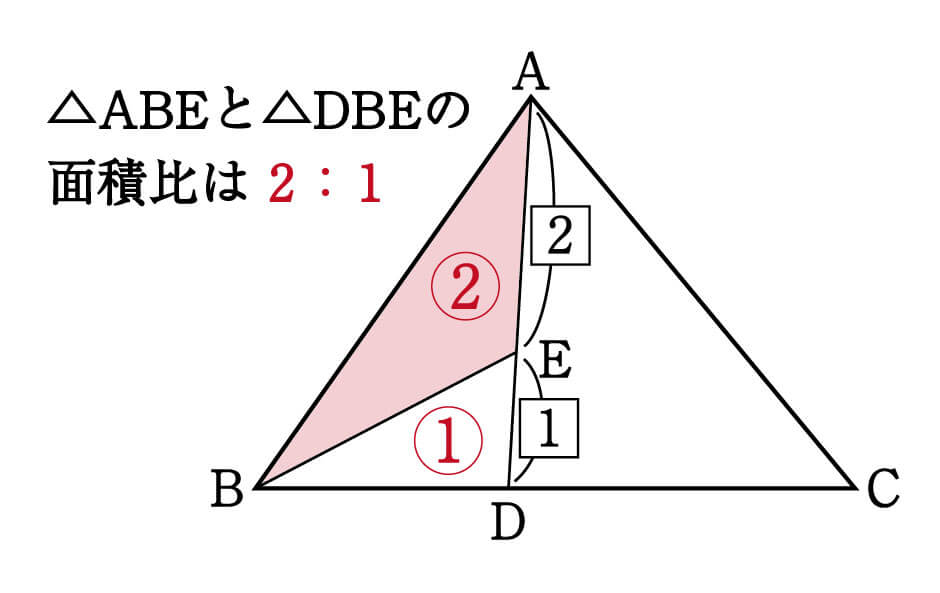
三角形の左側に注目すると、 ABEと BDEは「高さが同じ隣り合う三角形」であることがわかります。 ①の型に該当するので、2つの面積比は底辺比に等しい。 つまり ABE: BDE=2:1となるわけです。 続いて、 ABDと ACDを見てみると、こちらも①の型に当てはまります。 ABDの面積を、 ABEと BDEを合わせて3とした場合、 ABDと ACDの面積比は、底辺の比が3:5なので面積比の求め方を理解しよう こちらの記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。 人によっては三角形だと納得しにくいかもしれませんが、例えば正方形であればノートのマス目などを見てわかりやすいと思います。数学I 平面図形・空間図形の計量 図形の面積比・体積比 図形の面積比・体積比 相似な図形どうしでは面積比や体積比について、一定の法則が成り立つ。ここでは、相似な図形をもちいた平面や空間図形の計量について考えていこう。 相似と相似比 相似 2つの図形が相似 (similar) であるとは

質問 数学 中学 平行四辺形の中での面積比 オンライン無料塾 ターンナップ
数学 比例 面積
数学 比例 面積- 比をもとに{ bde}がsで表され,\ さらに{ ade}の面積sと合わせると{ abeの面積になる} { abeと abcはabを底辺とみるとそれぞれの高さはejとciである(右図)} {よって,\ その面積比はedとcdの比に等しいことを用いて abc}の面積が求まる 全体をsとする方針で求める\ 先に{ adcを求めるか abeを求めるかの2通り 面積比の求め方といっしょ。 つまり、 相似比の2乗の比 になってるのよ。 相似比が12の「円錐A・Bの表面積の比」は、 1^2 2^2 = 1 4 になるわけね。 もし、円錐Bの表面積が40 cm^2だったら、 円錐Aの表面積は10 cm^2 になるわけだね。 おめでとう! 相似比




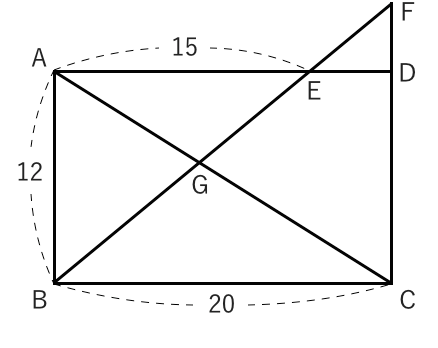
辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問
中学生のための数学学習支援、練習問題のダウンロード、家庭学習、定期テスト対策、受験勉強にお役立てください 中学・学習サイト ~勉強法と練習問題 英 数 国 理 社 top > 数学練習問題 > 面積比2 社会 歴史 練習問題;中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード・印刷 教材の新学習指導要領への対応について ただいま、ちびむすドリル中学生では、公開中の中学生用教材の新学習相似比が1:2 なら、 底辺も2倍 になるし、 高さも2倍 になるから、 2 2 で4倍 。 面積比は1:4 になるわけだよ。
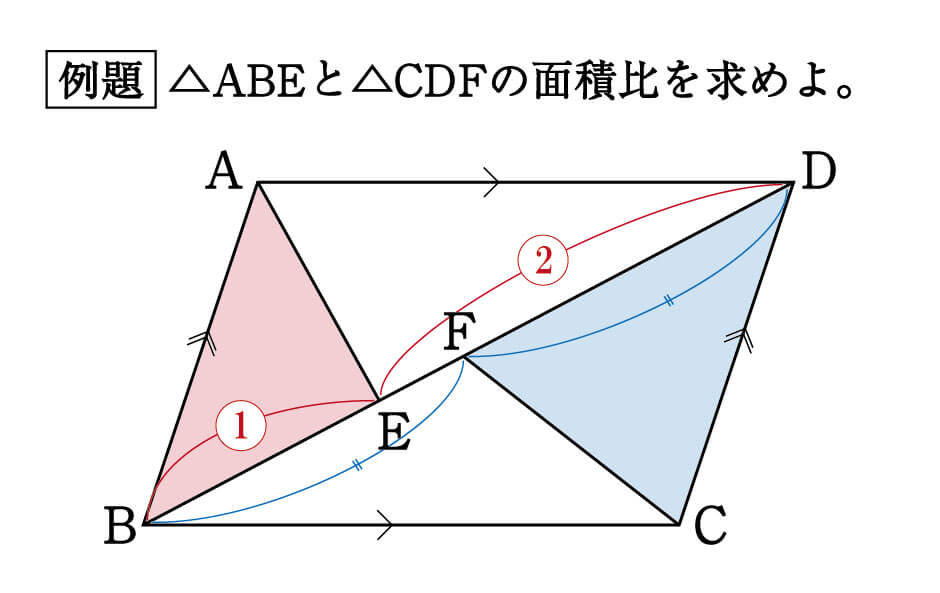
平行四辺形ABCDがあり、対角線BDを1:2にわける点がE、BDの中点がFとなっています。 このとき、 ABEと CDFの面積比を求めなさい、という問題です。 「面積比を求めなさい」という聞き方だけでなく、「 ABEは CDFの何倍か」「 CDFの面積が×× のとき、 ABEの面積を答えよ」といった形で問われることもあります。 こういった面積比を扱う問題が苦手な生徒には 16/2/29 /12/3 高校入試対策数学 スポンサーリンク 高校入試問題において、面積や面積比について求めさせる問題は、ほとんどの県や私立高校で出題されます。 今回は、面積比について便利な代表的なテクニックについて記述しています。 この記事 相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき
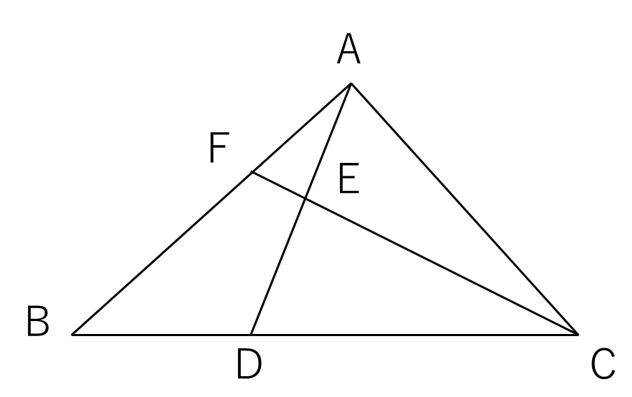
底辺の長さの比が、そのまま面積比となります。 問題を解いていく上で これら2つの特徴を利用していくことになるから しっかりと覚えておいてくださいね! 台形の面積比問題を解説! 三角形の面積比にまつわる公式たち 三角形の面積比,四面体の体積比にまつわる重要な公式を3つ紹介します。 → 三角形の面積比にまつわる公式たち フランク・モーリーの定理の証明 フランクモーリーの定理: 任意の三角形 a b c abc a bc に対して,3つの角の三等分線どうしが最初に 三 角 形 の 面 積 ① ( 三 角 形 A B X の 面 積 M ( ①)) = S × m m n × x x y ・・・(⭐︎3) 三 角 形 の 面 積 ③ ( 三 角 形 A C X の 面 積 N ( ③)) = S × n m n × x x y ・・・(⭐︎4) これらから、面積の比を作ると、 (三角形ABXの面積 M (①)) (三角形ACXの面積 N (③)) = S × m m n × x x y S × n m n × x x y この比を簡単にすると、 M N = m n



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




中学3年の数学 動画 相似と面積 基本編の問題 19ch
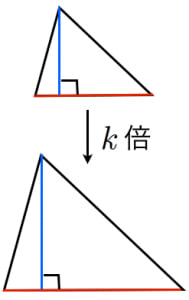
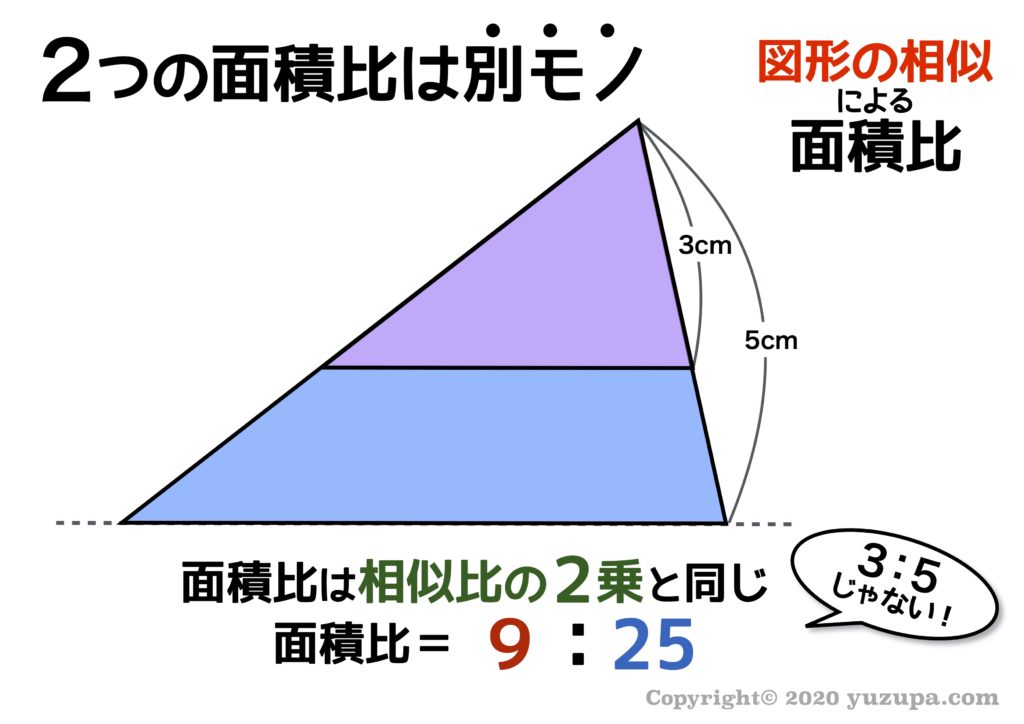
相似な平面図形の面積比 全て同じことですが,いろいろな言い方があります。 面積比=相似比の二乗 相似比が a b ab a b のとき,面積比は S a S b = a 2 b 2 S_aS_b=a^2b^2 S a S b = a 2 b 2 図形を k k k 倍に拡大すると面積は k 2 k^2 k 2 倍になる線分比と面積比の性質を使った問題です。 基本となるのは線分比です。 与えられた情報から新しい情報を導くことが基本となることは変わりません。 夢を叶える塾 数学を通して夢を叶える力を育む米沢市の学習塾 フォローする 夢を叶える塾 簡単なご案内;相似な図形の面積比 相似な図形の面積の比は「相似比の \(2\) 乗の比」になります。 つまり、 相似比 \(ab\) の図形の面積の比は \(a^2b^2\) です。 なので 面積の比は \(a×ab×b\) となるわけです。 もちろん、三角形だけでなく、円や四角形や五角形やその他なん



相似な図形 面積比の問題 苦手な数学を簡単に




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問
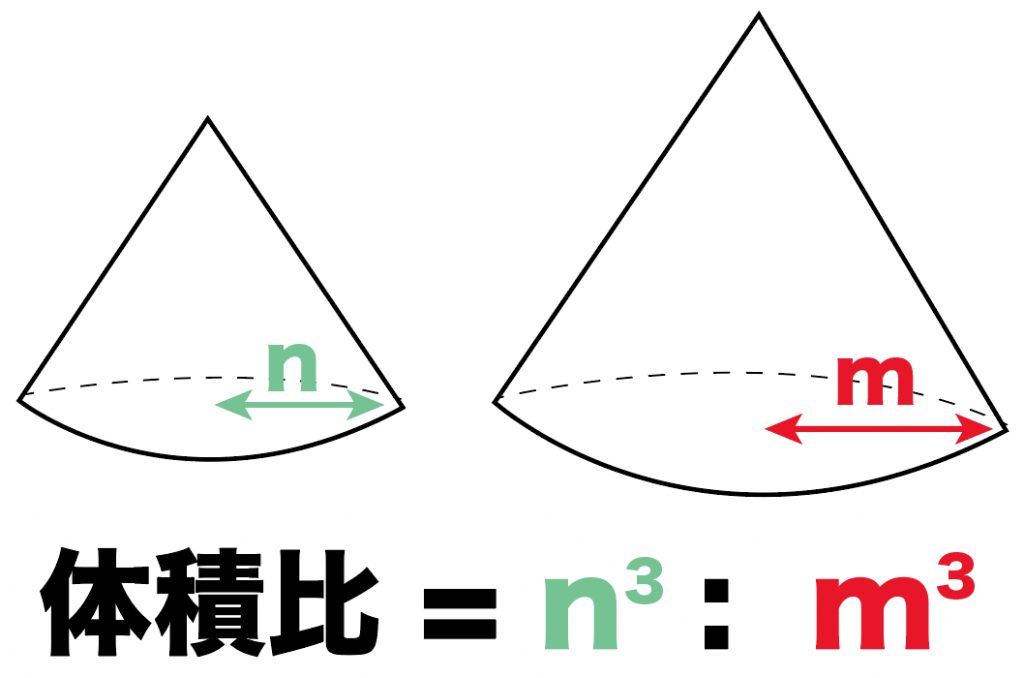
「面積比」は「相似比の2乗」になる ってやつだ。 たとえば、 ABCと A'B'C'の相似比が「nm」だとしよう。 このとき面積比は、 n² m² になってるんだ。 せっかくだから、この面積比の公式をつかってみよう。 つぎの2つの三角形をイメージしてみて。Defの面積は abcの面積の何倍か。 a b c d e f 図でaddb=13, beec=32である。 a b c d e f affeを求めよ。 afdと四角形dbefの面積比を求めよ。 図でapbp=21, bqqc=31, arrc=14である。 a b c p q r abc aprの面積比を求めよ。 abc bpqの面積比を求めよ。 abc pqrの面積比を求めよ。長さの比は相似比と同じ。 面積比は相似比の2乗。 体積比は相似比の3乗。 相似比がabの相似な図形の場合 辺、高さなど 長さの比は a b 表面積など 面積比は a 2 b 2 体積比は a 3 b 3 例 相似比23の相似な円柱PとQがある。 2h 2r 3r 3h




平面図形の苦手を解消 三角形の面積比 基本編




数学問題 知っている人は5秒で解ける三角形の面積比 暇つぶしに動画で脳トレ
底辺の長さの比が面積比となります。 よって、面積比は1:3なので rdqの面積は3 pqdの面積は4とわかります。 次に面積比 ABM ABCを求めよ。 A B C M ADDB=AEEC=11, DFFC=EFFB=12である。 A B C D E F 面積比 DFE DFBを求めよ。 面積比 ADE DBEを求めよ。 面積比 DFE ABCを求めよ。 次の問いに答えよ。 DがBCの中点、EがADの中点のとき面積比 AEC ABCを求めよ。 A B C D E BDDC=43, AEED=23のとき、面積比 EDC ABCを求めよ。「角を共有する三角形の面積比は線分の積の比に変換できる」 と覚えておきましょう。 この公式の頻出応用例として, A D E ADE A D E と四角形 B D E C BDEC B D EC の面積比を求める問題も多いです。
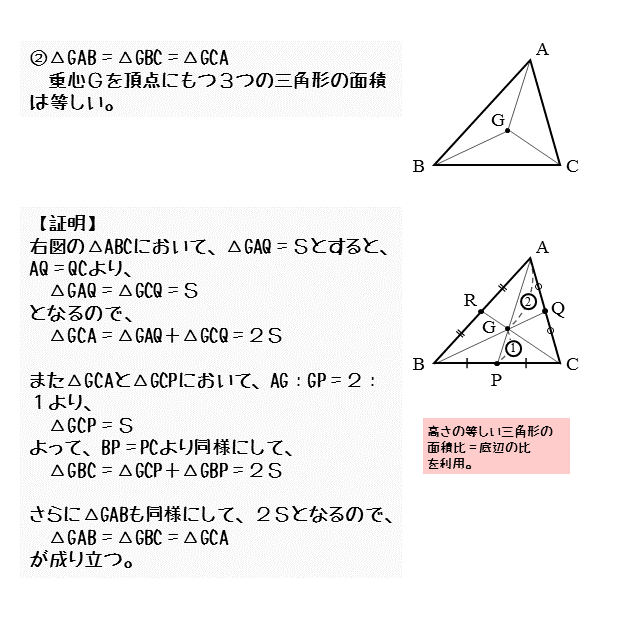



図形の性質 重心について 日々是鍛錬 ひびこれたんれん



Studydoctor線分の比と面積比 中学3年数学 Studydoctor
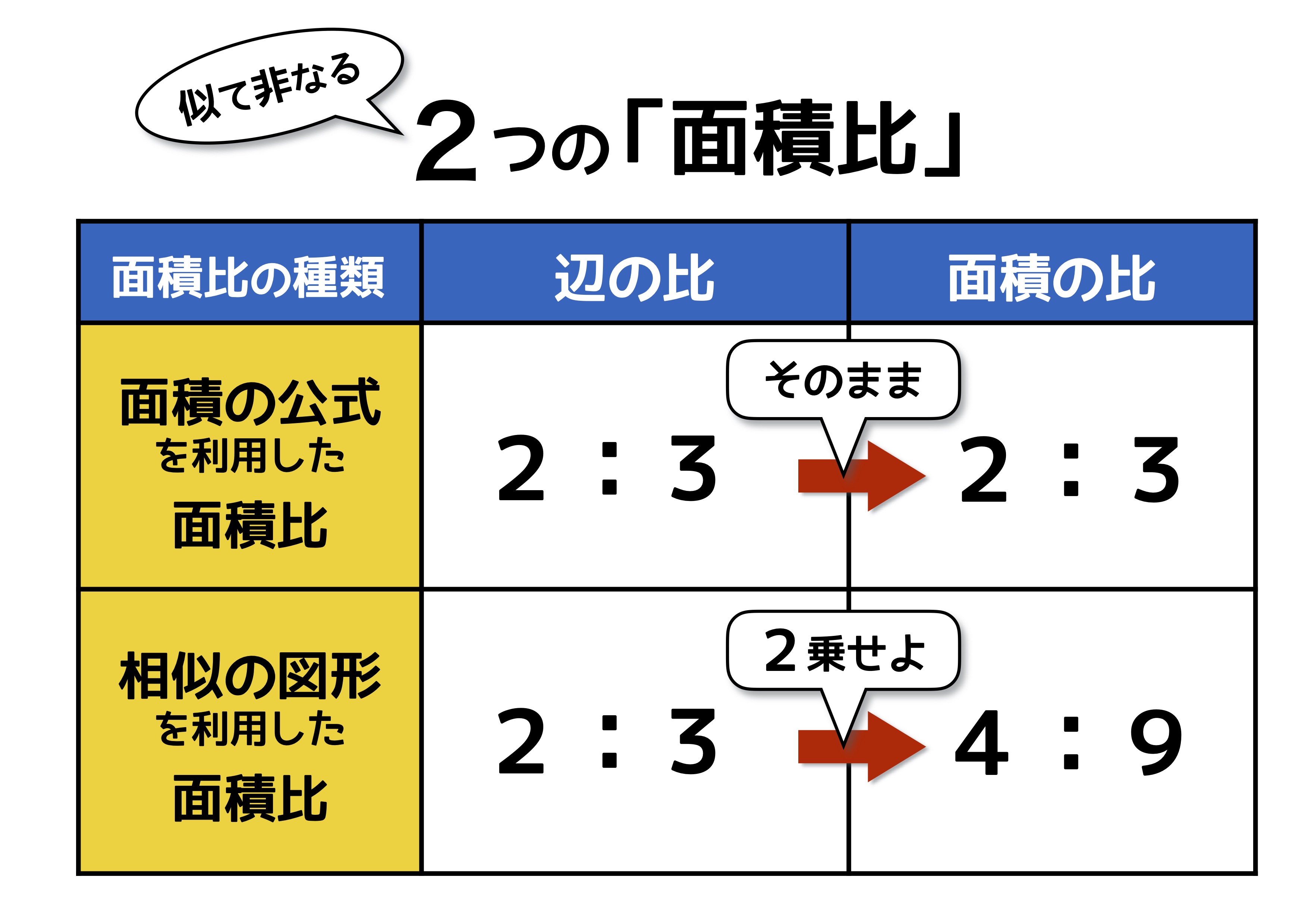
全体の面積×キュウリの比をすれば答えが出る。 360×5/12=150 150㎡ トマトの面積は 全体の面積からキュウリの面積を引いた残りになる。 360―150=210 210㎡ 面積が60㎡と80㎡の2つの花壇の草取りを、生徒28人でします。広さの割合で分かれるとすると、何人と さらに、別の面積比を考えてみるかのぉ ピンクと緑の面積比は、CEとAEの線分比で表現できるわけじゃ ここでは分数の形で書いておくと \( \frac{三角形BCX}{三角形ABX} = \frac{CE}{AE} = \frac{2}{1} \) ・・・(式3)の面積を として、比例式を作ると よって、 の面積は ㎠ となります。 面積比と聞かれたら、何でもかんでも2乗して面積比を作っちゃう人がいるので気を付けてくださいね。 2乗が使えるのは相似な図形
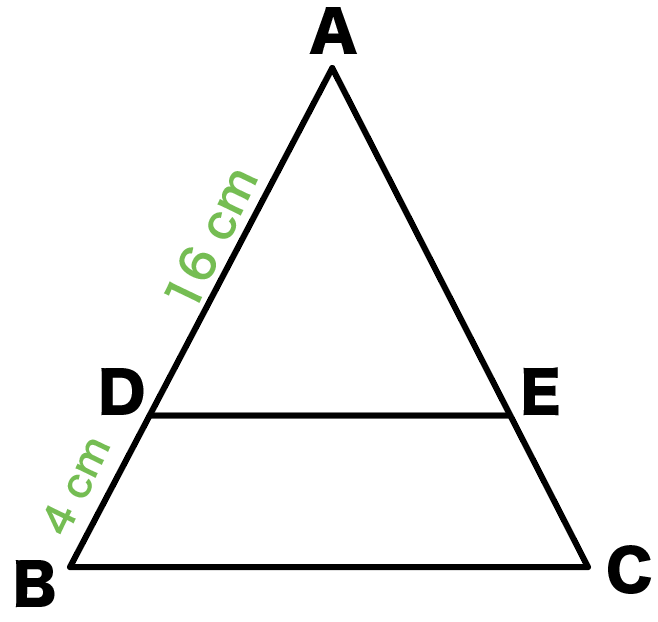



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
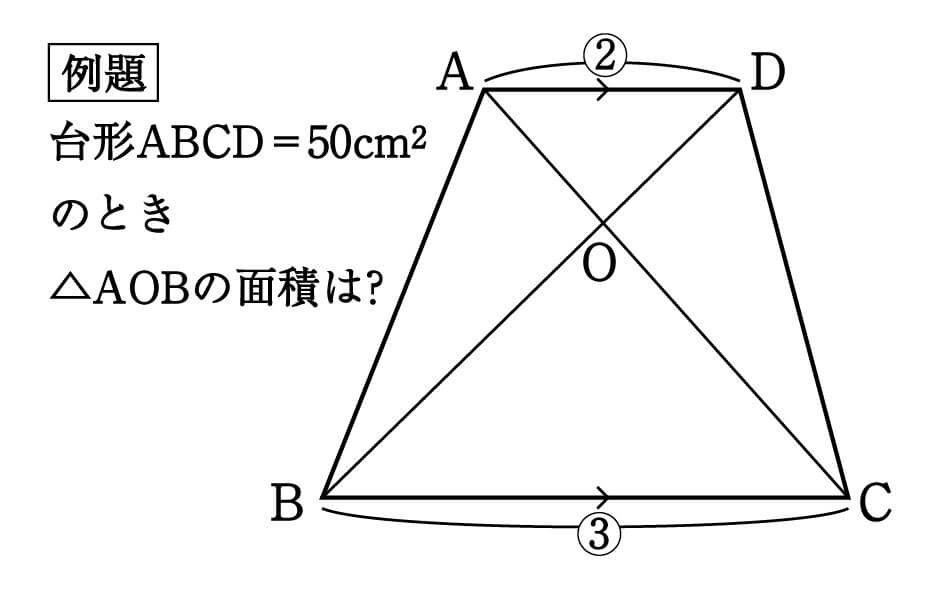
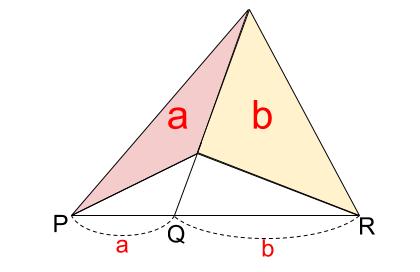
基本は、高さが同じ三角形の面積比を使う 例えば 次のような図がある場合、 APCの面積は ABCの面積の何倍になるか 分かるでしょうか? ※図中の数字は、辺の比を表します。 この場合は、 高さが同じ三角形の面積比は 底辺の長さの比と同じになる 台形abcdがあり、上底adと下底bcの比は2:3です。 台形の面積が50cm 2 であるとき、 aobの面積はいくつでしょうか? という問題です。 問題文には‟面積比"という言葉が使われていませんが、2つの異なる図形の面積を比べる問題なので、これも面積比のパターンの1つです。 ABEと ADEの面積比は、底辺比と同じなので1:2。 つまり、 ABEは ABDを3等分したうちの1つ分なので、以下のように表せます。 \( ABE\)の面積\(=\displaystyle \frac{1}{2}S×\frac{1}{3}=\frac{1}{6}S\)




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
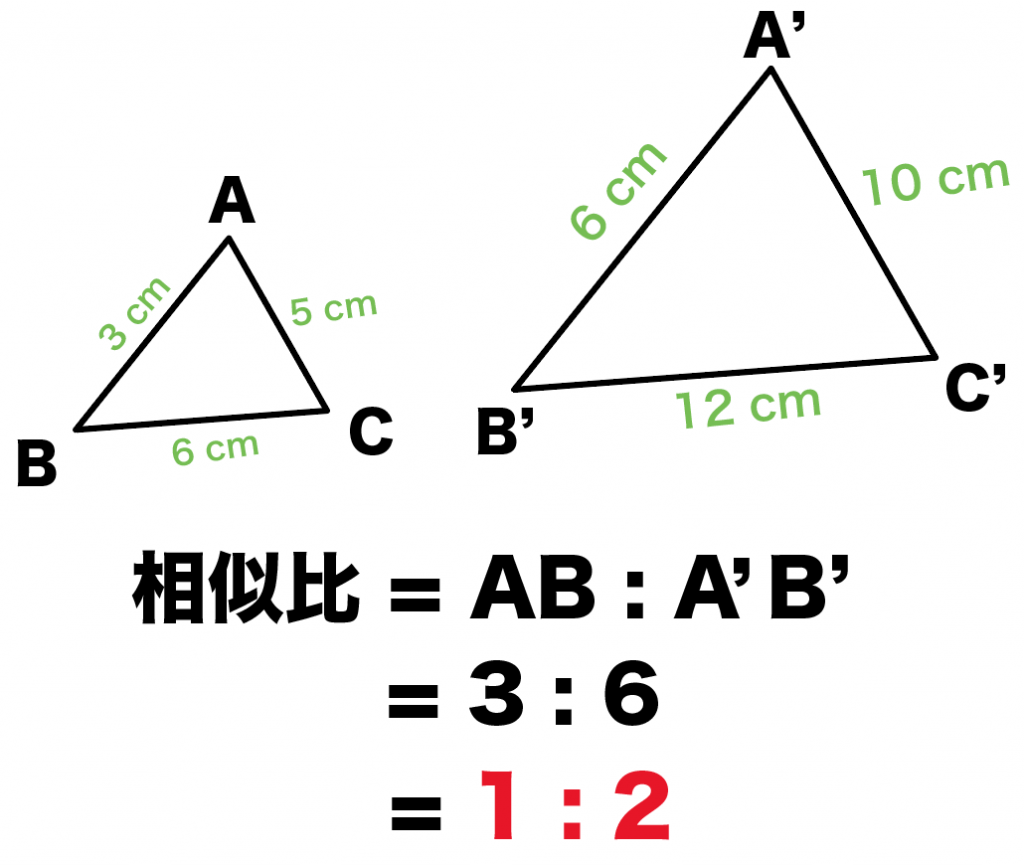



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく
中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード・印刷 基本的な立体の相似の意味と、相似な図形の相似比と面積比、および体積比の関係について理解し、問題で練習します。それぞれの面積の比を考える。 ということを問題で問われているのですね! だから、それぞれの面積をどのように求めていくか。 これがポイントとなります。 問題の解答! どの三角形も形が斜めになっていて 底辺と高さをとるのが難しいですね。 こういうときには 全体から削り取る! とつまり面積比は、「 高さが等しければ底辺の比、底辺が等しければ高さの比になる 」ということです。 今となっては、この公式 $2$ つが本質的に同じである理由がわかるのではないでしょうか。




面積比



1
実は、 1つの角が等しい三角形の面積比は、その角をはさむ2辺の積によって求められます。 abc: ade=ab×ac:ad×aeと覚えておきましょう。 三角形の面積比のまとめ ここまで、三角形の面積比について解説してきました。



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学 高校までの三角形の面積と面積比についてまとめました 高校生 数学のノート Clear



3分でわかる 相似比から体積の比 表面積比を求める公式 Qikeru 学びを楽しくわかりやすく




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



1




高校入試対策数学 面積比に関する対策問題 Pikuu




高校数学a 三角形の面積と線分の比 練習編 映像授業のtry It トライイット




平面図形をマスター 三角形の面積比 応用編その3




中3 数学 6 7 相似比と面積比 平行四辺形 Youtube



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




面積比 2つの三角形で高さが同じときの面積比 身勝手な主張



1




相似比と面積比 中学3年数学 Youtube



相似 平行四辺形と面積比の問題を徹底解説 数スタ




相似じゃない三角形の面積比の求め方がよく分かりません Clear



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




平面図形 面積比 開成中2018年 算数 数学 受験 算太数子 う山雄一先生 統括ブログ




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




中3数学 相似な図形の表面積比 体積比 映像授業のtry It トライイット



中学生数学相似な図形の相似比と面積比について画像の正方形abcdで 辺bc Yahoo 知恵袋



メネラウスの定理 最終奥義 高校数学の無料オンライン学習サイトko Su




大至急です 相似 面積比の問題です Clear




質問 数学 中学 平行四辺形の中での面積比 オンライン無料塾 ターンナップ



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




中3数学 図形と相似27 相似な図形の面積比 すべて無料 星組の中学数学講座



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor




中3数学 相似な図形の面積比 練習編 映像授業のtry It トライイット



面積比とは 1分でわかる意味 公式と求め方 問題 三角形と四角形の関係



相似比と面積比 体積比の公式の証明 高校数学の美しい物語




中学校数学 証明のコツ 面積比 体積比




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext




平面図形の苦手を解消 三角形の面積比 基本編
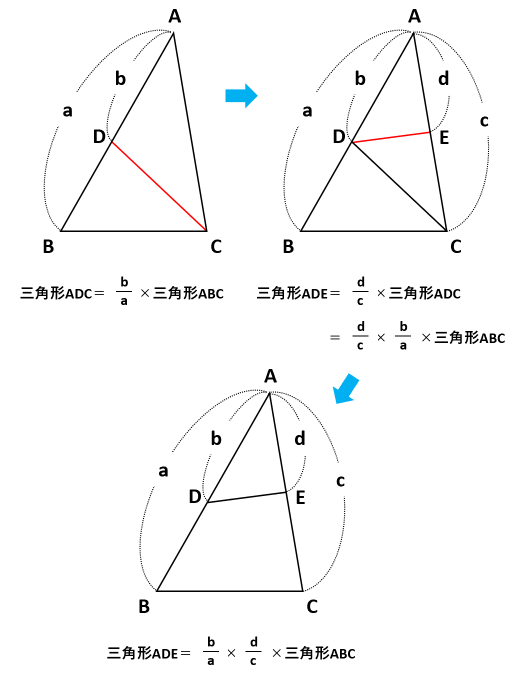



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



三角形の面積比の問題 Of 京極一樹の数学塾会員頁



三角形 四角形の面積比 中学から数学だいすき




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学
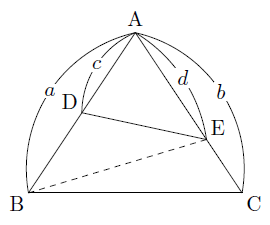



1角共有の三角形の面積比 まなびの学園




辺の比と面積比問題 考え方1 Youtube




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋




三角形の面積比 数学の偏差値を上げて合格を目指す




中3数学 相似な図形の面積比 映像授業のtry It トライイット




中学 数学 テクニック 三角形の面積比を使って辺の比を出す 高校入試 高校受験 裏ワザ Youtube




相似の面積比を求める問題 上級編 Youtube
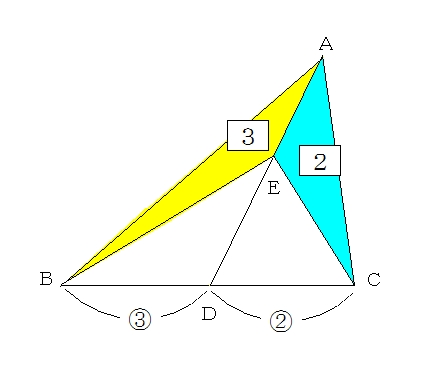



辺の比と面積比



算数 線分比と面積比 数学 中学受験専門 ともや塾




成績アップの秘訣 自学学習のススメ 数学の三角形の相似比 ピラミッド型と砂時計型 幼児教育 児童教育




これでバッチリ 相似の面積比を求める問題をイチからやってみよう 数スタ




三角形の面積比と相似比 チーム エン




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生
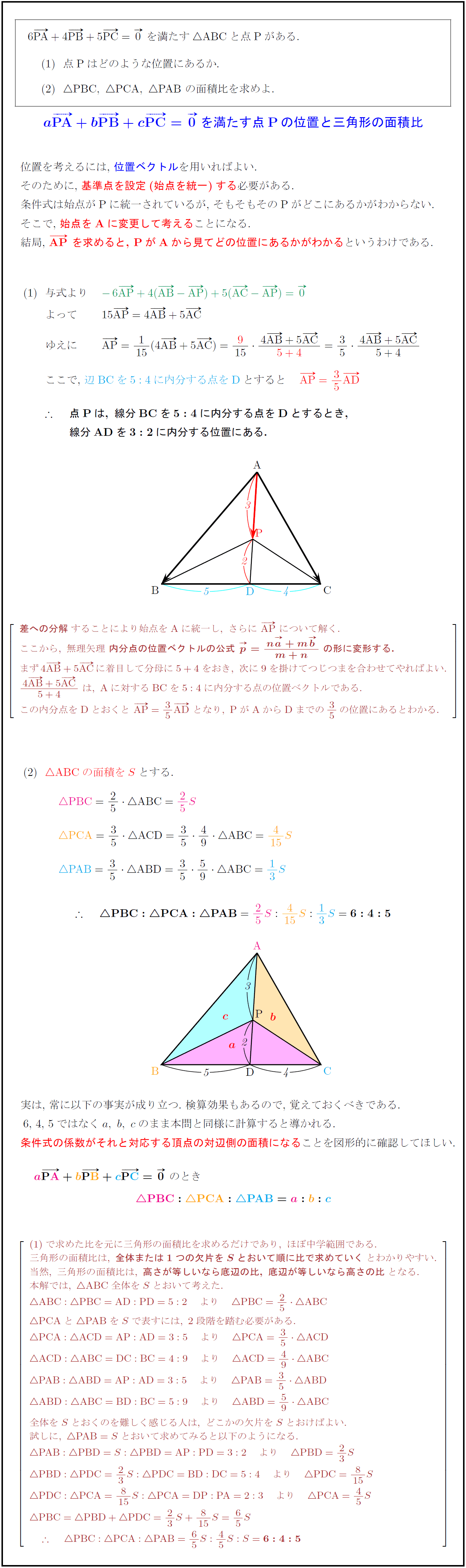



高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月




平面図形をマスター 三角形の面積比 応用編その3




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su



3




数学 中3 53 相似と面積 応用編 Youtube




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
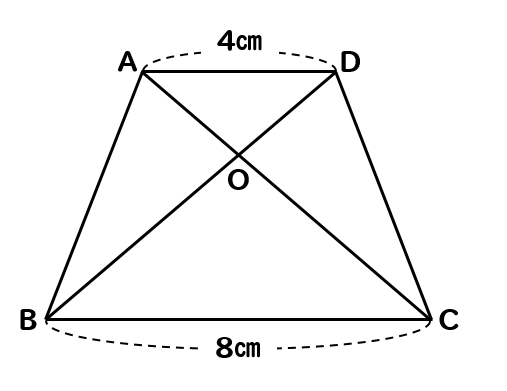



相似 台形と面積比の問題を徹底解説 数スタ
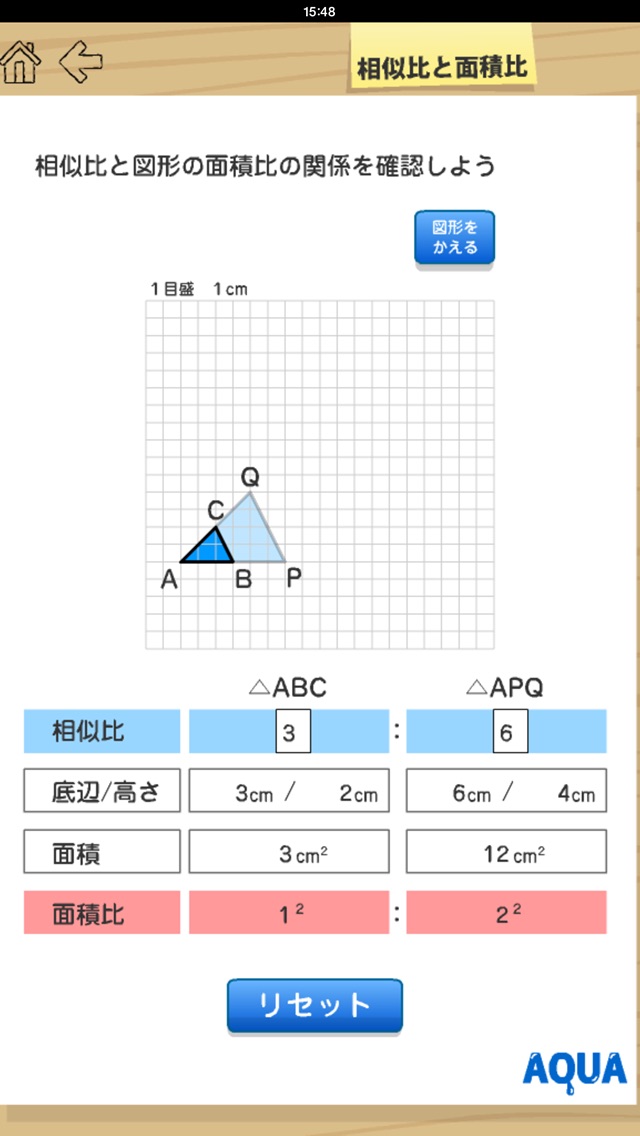



相似比と面積比 さわってうごく数学 Aquaアクア Iphoneアプリ Applion




三角形で面積比と底辺の比の関係は 平面図形分野の頻出問題を考える みみずく戦略室




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube



Studydoctor台形の面積比 中学3年数学 Studydoctor
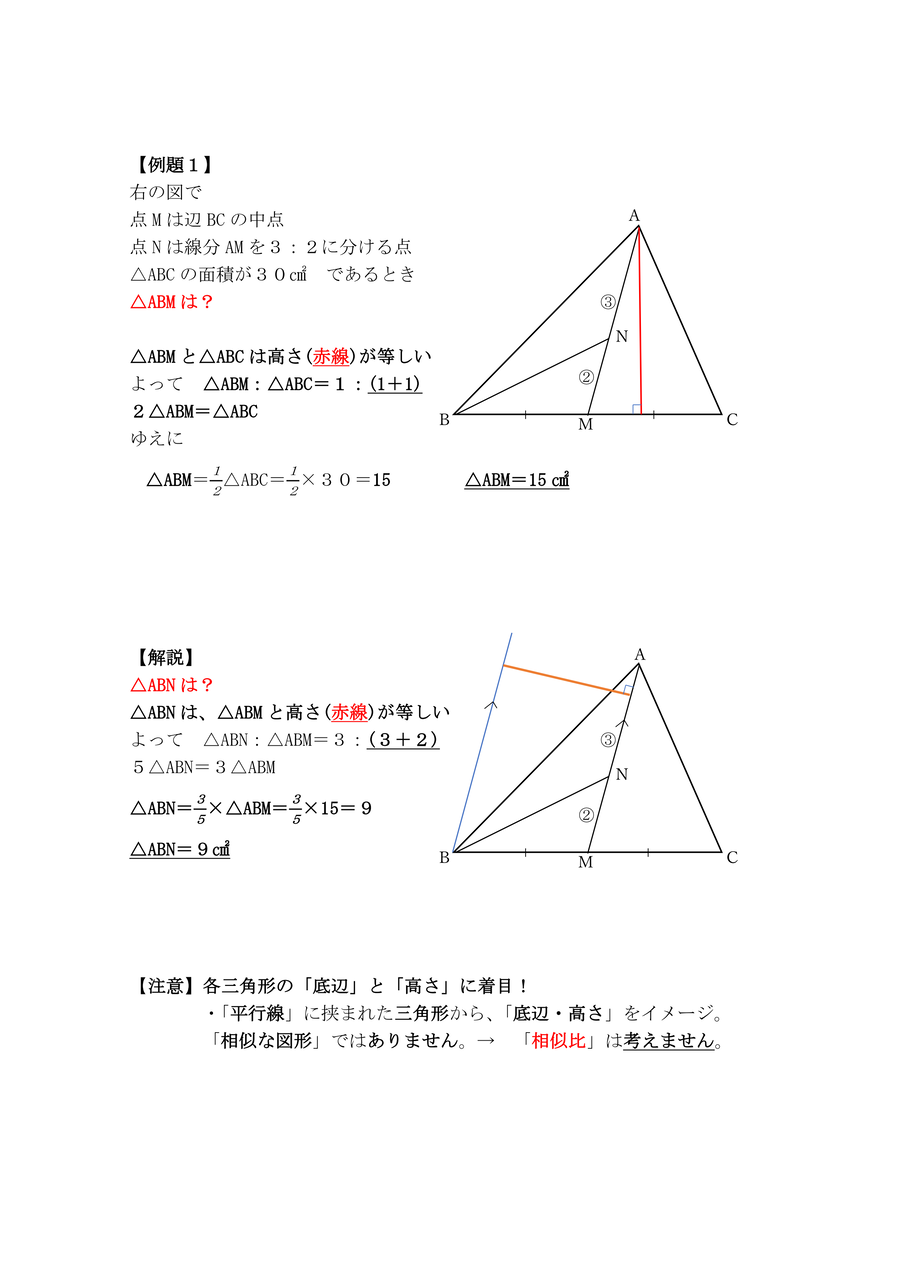



中学校数学 証明のコツ 面積比 体積比
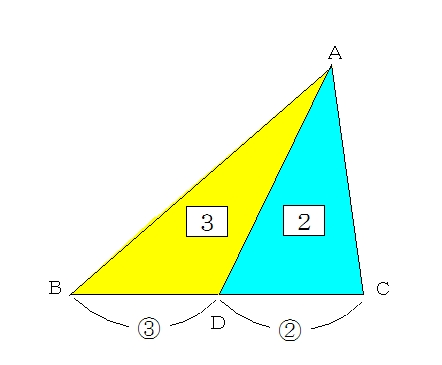



辺の比と面積比



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



面積が何倍かを求める問題 応用編 苦手な数学を簡単に




ベクトル方程式による面積比の問題と解き方



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 暇つぶしに動画で脳トレ




面積比 19都立 数学カフェjr




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



公立高校入試2019 図形 中学から数学だいすき
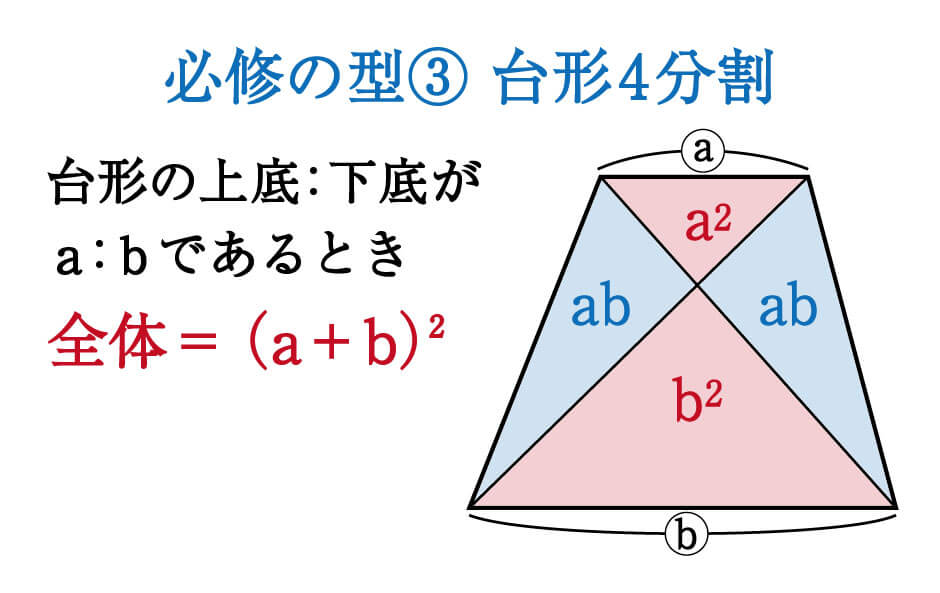



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中3数学相似問題 この問題の面積比の求め方がよく分かりません 教えてください Yahoo 知恵袋




世界一わかりやすい数学問題集中3 5章 図形と相似



ややこしや 線分の比 と 面積の比 名寄 算数数学教室より




高校入試数学 入試によく出題される代表的パターンまとめ




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



数学i Aチェック リピート 第4章 2図形への応用 8 相似形の面積比 Pukiwiki




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



高校入試数学 面積比のポイントと練習問題




平面図形をマスター 三角形の面積比 応用編その3
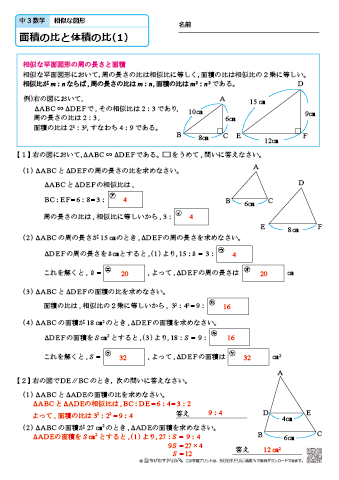



中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




平面図形をマスター 三角形の面積比 応用編その3
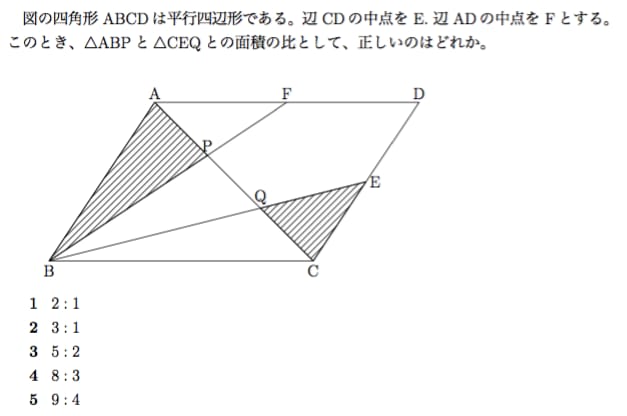



平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題
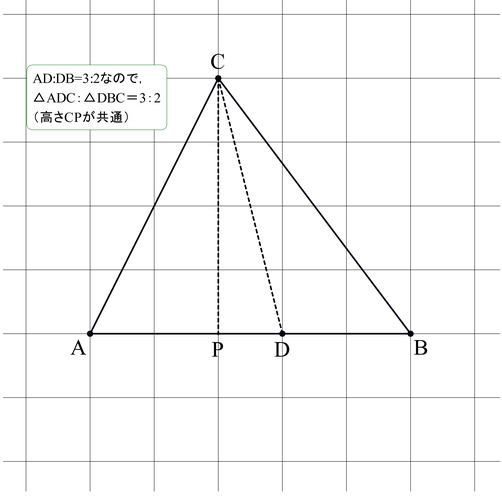



線分比と面積比 クソオリジナル問題 高校入試 数学 良問 難問




高校数学a 三角形の面積比 等高 等底 等角 受験の月



0 件のコメント:
コメントを投稿